1 1. El factor que se repite y se multiplica se denomina

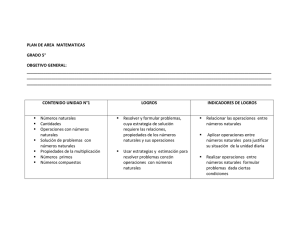
PLAN DE REFUERZO
Fecha:
Dia
11
Mes
09
Año
PERIODO: III
2015
META DE COMPRENSIÓN: Desarrolla comprensión acerca de
la potenciación y sus operaciones inversas como representación AREA: Matemáticas
de los números naturales.
COLEGIO
BETHLEMITAS DOCENTE: Nora Patricia Barrera Gómez
NOMBRE ESTUDIANTE:
ASIGNATURA: Aritmética
Nº
GRADO: 5º
A
B
1. OBSERVACIONES Y RECOMENDACIONES:
El siguiente plan de refuerzo contiene la ejercitación básica de los tópicos desarrollados
durante el período. Se debe tener en cuenta para su realización las guías de desarrollo e
informativa trabajadas, los apuntes de clase, las guías de control corregidas y los referentes
bibliográficos que encontrará al final del plan. La metodología bajo la cual se desarrollará este
consiste en el desarrollo guiado -por el docente. La participación en la jornada de
retroalimentación y el desarrollo del plan de refuerzo equivale al 20% del porcentaje total de la
nota de recuperación. (El estudiante debe presentarse a la retroalimentación con su respectivo
plan de refuerzo impreso), la asistencia a dicha retroalimentación será de obligatorio
cumplimiento para todos los estudiantes que hayan reprobado alguna de las asignaturas. Si el
estudiante no se presenta a la jornada de retroalimentación, se asume como juicio valorativo
1.0 y se deja constancia en el anecdotario en “Atención especializada”. (SIEE Art 2, Nota 2)
1. IDENTIFICACIÓN DE TÓPICOS:
Varias veces el mismo número
2. DESARROLLO CONCEPTUAL:
POTENCIACIÓN
Una Potencia es el producto de n factores iguales.
Los elementos que intervienen en la potencia son tres:
1. El factor que se repite y se multiplica se denomina Base.
2. El numero que está en la parte superior derecha y que nos
indica, cuantas veces debemos multiplicar la Base, se
denomina, Exponente.
3. El resultado se denomina, Potencia.Como aparece en la figura.
Se lee , dos elevado a la tercera potencia y es igual a
2x2x2=8
RADICACIÓN
La radicación es la operación inversa a la potenciación.
Los elementos que intervienen en la radicación:
1. Índice, corresponde al número que se le asigna al radical.
En el caso de la figura es el número dos y entonces
se leerá Raíz cuadrada.
2. La cantidad que se ubica dentro del radical, se
denomina cantidad subradical o Radicando.
3. El resultado, es la raíz (n) del radicando.
1
Para calcular la raíz de determinado número, se hace la descomposición en factores primos
de la cantidad subradical:
Calcular √
22
22.32.32
32
Con base en los factores
obtenidos, se hacen
grupos de acuerdo a la
cantidad que indique el
índice de la raíz
32
Luego, se reemplaza el producto obtenido y se cancelan los exponentes con el valor del
radical.
= √
=2.3.3 = 18
√
LOGARITMACIÓN
Es la operación matemática inversa a la potenciación, con ella es posible hallar el exponente
si se conoce la base y la potencia.
El logaritmo que observamos en el ejemplo se lee:
Logaritmo en base 2 de 8 es igual a 3.
Para calcular el logaritmo de determinado número, se descompone la potencia por el número
que indique la base:
Calcular Log 5 625
54
Como en la logaritmación
se busca el exponente, se
observa de acuerdo a la
descomposición, cuántas
veces se repite la base.
Por lo tanto Log 5 625 = 4
2
RELACIÓN ENTRE LAS TRES OPERACIONES
3. EJERCITACIÓN
1. Completa la siguiente tabla:
PRODUCTO DE
OPERACIÓN
FACTORES
5X5X5
43
EXPONENTE
BASE
POTENCIA
125
4
3
2. Encuentre la potencia: 29
3. Escriba el número correcto en cada recuadro.

a) 25 =625
b) 8 2 = 
4. Resuelve los siguientes ejercicios utilizando la propiedad respectiva:
 
a. 2 2
3
c. 10 45  10 43
b. 32 x31
5. Encuentra el resultado de las siguientes raíces y justifica.
a. √
b. √
6. Resuelve los siguientes problemas:
a. Un terreno cuadrado tiene 26m de lado. ¿Cuál es su área?
b. ¿Cuál es la medida del lado de un cuadrado cuya área es 100m2?
7. Calcula el lado de cada uno de los cuadrados cuya área se indica. Observa el ejemplo.
8. Calcula los siguientes logaritmos:
a. Log 6 1296
b.
8. Completa la tabla
POTENCIACIÓN
57=78125
RADICACIÓN
√
LOGARITMACIÓN
=4
=2
3
4. METODOLOGÍA DE ESTUDIO PROPIAS DE LA ASIGNATURA:
Busca un lugar tranquilo, libre de ruidos y de distracciones, donde puedas estudiar; consigue una
buena cantidad de hojas de borrador donde puedas escribir y desarrollar ejercicios, mejor aún sería
un cuaderno para que tengas todo más ordenado y por último, al desarrollar una situación y/o
ejercicio pregúntate siempre ¿qué me dan?, ¿qué me piden?, ¿puedo hacer una gráfica o diagrama?,
¿qué tengo que averiguar para poder llegar a lo que me piden?, esto te ayudará mucho a centrar tus
ideas para la resolución.
Desarrolla nuevamente y entiende los ejemplos vistos en clase. Lo principal aquí es entender,
preguntarse ¿por qué se realiza tal o cual operación? No se trata de memorizar pasos y nada más,
sino de entender los porqués de cada cosa.
Cuando te aparezcan las dudas tienes que tratar de resolverlas por ti mismo buscando libros,
leyéndolos, repasando la teoría, etc.; si después de esto no pudiste despejarlas, pregunta a tu
profesora. Este esfuerzo por tratar de resolver la duda por ti mismo no es una pérdida de tiempo, más
bien te hace razonar, investigar y, por tanto, aprenderás.
5. BIBLIGRAFIA
 LEON BELTRAN, Gloria Patricia. Aventura Matemática. Grupo editorial Norma. Bogotá:
1998
 LEGUIZAMÓN DE BERNAL, Cecilia. Conexiones Matemáticas 6º. Grupo editorial Norma.
Bogotá: 2006.
 MEJÍA FONSECA, Cristina Fernanda. Desafíos matemáticas 6º. Bogotá: Grupo Editorial
Norma, 2001.
 SILVA CALDERÓN, Luz Helena. Matemáticas para pensar 5º. Bogotá: Grupo editorial
norma, 2011.
 CENTENO ROJAS, Rocío. ZOOM a las matemáticas. Bogotá: Grupo Editorial Norma,
2013.
4